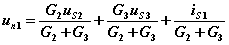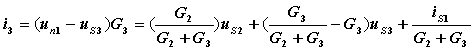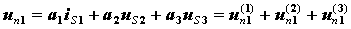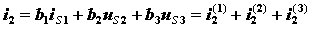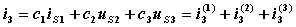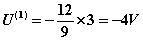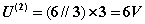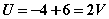西门子一级|驱动器总代商|2023

选结点电压为未知量,可以减少方程个数。结点电压自动满足KVL,仅列写KCL方程就可以求解电路。各支路电流、电压可视为结点电压的线性组合。求出结点电压后,便可方便地得到各支路电压、电流。 2.方程的列写 …… 其中: |
1.叠加定理的内容 图1 图1所示电路应用结点法: =三个电源共同作用is1单独作用++us2单独作用us3单独作用图2 3) 功率不能用叠加定理计算(因为功率为电压和电流的乘积,不是独立电源的一次函数)。 例4-1图 解:应用叠加定理求解。首先 画出分电路图如下图所示 当12V电压源作用时,应用分压原理有: 5. 齐性原理 |
1. KCL的独立方程数 对图中所示电路的图列出4个结点上的KCL方程(设流出结点的电流为正,流入为负): 结点① 结点② 结点③ 结点④ 把以上4个方程相加,满足:①+②+③+④=0 |
- 西门子plc模块|驱动器总代理|2023 2023-10-26
- 西门子plc模块-驱动器代理 2023-10-26
- 西门子cpu模块-驱动器代理 2023-10-26
- 西门子一级-驱动器代理 2023-10-26
- 西门子cpu模块-驱动器代理商 2023-10-26
- 西门子一级-驱动器代理商 2023-10-26
- 西门子plc模块|驱动器总代理商 2023-10-26
- 西门子cpu模块|驱动器总代理商 2023-10-26
- 西门子一级|驱动器总代理商 2023-10-26
- 西门子plc模块|驱动器总代理 2023-10-26
- 西门子cpu模块|驱动器总代理 2023-10-26
- 西门子驱动器-变频器代理商-2023 2023-10-26
- 西门子驱动器-模块代理商-2023 2023-10-26
- 西门子驱动器-授权代理商-2023 2023-10-26
- 西门子驱动器-plc模块代理商-2023 2023-10-26
联系方式
- 地址:上海杨浦 上海市松江区广富林路4855弄88号3楼
- 邮编:200093
- 电话:15821971992
- 经理:聂聪
- 手机:15821971992
- 传真:021-33556143
- QQ:2724917714
- Email:2724917714@qq.com