西门子PLC代理商6ES7215-1BG40-0XB0

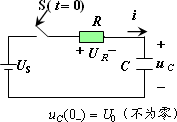
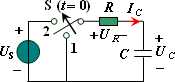
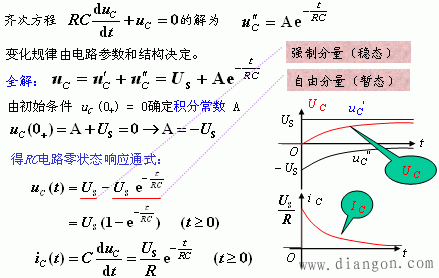
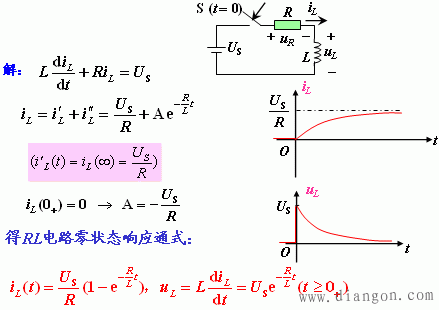
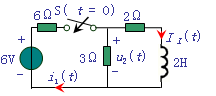
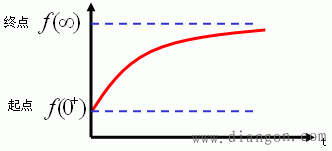
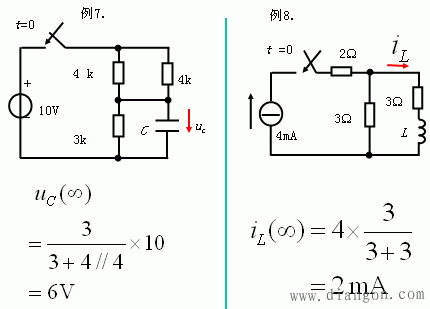
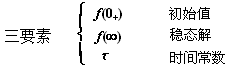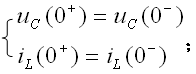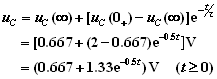引起电路响应的因素有两个方面,一是电路的激励,而是动态元件储存的初始能量.当激励为零,仅由动态元件储存的初始能量引起的响应叫零输入响应；当动态元件储存的初始能量为零,仅由激励引起的响应叫零状态响应；两个同时引起的响应叫全响应.

零状态响应是指在t=0-时，电容器的电压为0，电感器的电流为0；
零输入响应是指在t=0-时，电源的输入为0；下面早点介绍一阶电路的全响应。

全响应：非零初始状态的电路受到外加激励时电路中产生的响应，称为全响应。
　　1.RC电路的全响应的分析

　　　
　　（非齐次微分方程）
　　
　　解答为：uC = uC' + uC''

　　得RC电路的全响应的通式：
　　2.RC电路的全响应通式的两种分解方式
　　（1）全响应(complete response)
　　= 强制响应(forced response)+自由响应(natural response)
　　= 稳态响应(steady-state response) +暂态响应(transient response)

　　（2）全响应= 零状态响应 + 零输入响应

　　全响应小结:
　　（1）全响应的不同分解方法只是便于更好地理解过渡过程的本质；
　　（2）零输入响应与零状态响应的分解方法其本质是叠加，因此只适用于线性电路；
　　（3）零输入响应与零状态响应均满足齐性原理，但全响应不满足。

]

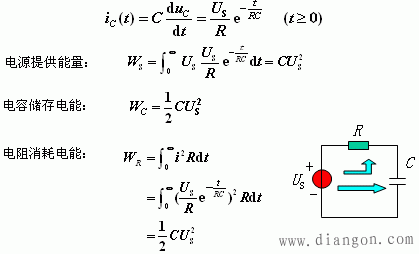
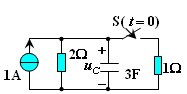
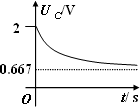
电路中含有一个独立的储能元件（电容或电感）的称为一阶电路.
若输入的激励信号为零,仅有储能元件的初始储能所激发的响应,称为零输入响应.
反之,电路的初始储能为零,仅由激励引起的响应为零状态响应.
动态电路,电源.电感或电容的初始储能均能作为电路的激励引起响应.

零状态响应（zero-state response）：
　　电路在储能元件零初始条件下由外施激励引起的电路响应。
　　
　　1.RC电路的零状态响应

　　t < 0时，开关S在位置1，处于稳态，即：uC(0-) = 0。
　　t = 0时，开关S打向位置2，列方程：
　　一阶常系数非齐次线性微分方程
　　
　　：特解（强制分量）
　　与输入激励的变化规律有关。当某些激励的强制分量为电路的稳态解时，强制分量又称为稳态分量。
　　（1）求稳态分量即特解
　　和外加激励信号具有相同的形式。
　　
　　在该电路中，令＝K（常数）
　　代入方程　　得　　
　　
　　在电路中，通常取换路后的新稳态值 [记作：]作特解，故此特解也称为稳态分量。
　　所以该电路的特解为：
　　（2）求：通解（自由分量，暂态分量）
　　
能量关系
　　

电源提供的能量一半消耗在电阻上，一半转换成电场能量储存在电容中，也就是说，充电效率为50%。
　　2.RL电路的零状态响应
　　已知iL(0-) = 0，求电感电流iL(t)。
　　
3.一阶电路零状态响应解的一般公式
　　一阶电路的零状态响应是由激励引起的响应，它实质上是动态元件的储能由零逐渐增长到某一定值的过程。
　　
　　(1)τ体现了一阶电路的固有特性，衰减快慢取决于时间常数τ。
　　RC电路τ = ReqC，RL电路τ = L/Req。
　　
　　(2)
　　例6. 如图所示电路，已知t < 0时电路处于稳态，t = 0时开关S闭合。求t > 0时的L、i1、u2。
　　

上式可写成：
　　在直流激励下，电路的任意一个全响应可用f(t)表示，则：
　　
　　一阶电路暂态分析的三要素法

　　
　　式中f(t)分代表一阶电路中任一电压、电流函数。
　　
　　结论
　　根据三要素，可直接写出一阶电路在直流激励下的全响应，这种方法称为三要素法。适用范围：激励为直流和正弦交流。
　　三要素法求解暂态过程要点：
　　（1）分别求初始值、稳态值、时间常数；
　　（2）将以上结果代入暂态过程通用表达式；
　　（3）画出暂态过程曲线（由初始值→稳态值）。
　　　（电压、电流随时间变化的关系）
　　
　　1.初始值的计算
　　步骤: （1）求换路前的
　　　　（2）根据换路定则得出：
　　　　（3）根据换路后的等效电路，求其它的或
　　2.稳态值的计算
　　步骤:（1）画出换路后的等效电路（注意：在直流激励的情况下，稳态时令C开路，L短路）；
　　　　（2）根据电路的解题规律，求换路后所求未知数的稳态值。
　　注: 在交流电源激励的情况下，要用相量法来求解。
　　求稳态值举例
　　
　　3.时间常数的计算
　　原则:要由换路后的电路结构和参数计算。(同一电路中各物理量的是一样的)
　　步骤:（1）对于只含一个R和C的简单电路，对于较复杂的一阶RC电路，将C以外的电路，视为有源二端网络，然后求其等效内阻 R'。则:
　　（2）对于只含一个L 的电路，将 L 以外的电路，视为有源二端网络,然后求其等效内阻R'。则:
　　RC 电路τ的计算举例
　　例9.