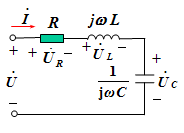
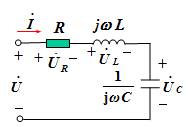
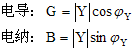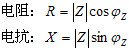如果线性受控源的控制电压或电流是正弦量，则受控源的电压或电流将是同一频率的正弦量。例如：

例1 正弦电流源 iS的有效值为5A，ω = 1000rad/s，R = 3Ω， L = 1H， C = 1μF。求uad和ubd。

解：画出电路的相量形式。设电流相量为参考相量(referencephasor)，即

则

例2. 已知右图中各电流表都是交流电流表，读数为电流的有效值。求电流表4、5的读数。

解： 选并联电压相量为参考相量。

小结：

1.求正弦稳态解是求微分方程的特解，应用相量法将该问题转化为求解复数代数方程问题。

2.引入电路的相量模型，不必列写时域微分方程，而直接列写相量形式的代数方程。

3.采用相量法后，电阻电路中所有网络定理和一般分析方法都可应用于交流电路。

导纳是复阻抗Z的倒数。用Y表示。

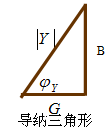
一般情况 G≠1/R　B≠1/X。

阻抗和导纳可以等效互换：ZY=1。

导纳适合于并联电路的计算，单位是西门子( s )。

1.Y和总电流、总电压的关系

导纳模:

导纳角:

2.单一元件的复导纳

正弦激励下

　感纳 　　　　　　容纳

3.Y和电路性质的关系（以RLC并联电路为例）

当信号角频率一定时，电路性质由参数决定。

当时，，表示 i 领先u，电路呈容性。

当时,，表示 i 落后u ，电路呈感性。

当时,，表示u ，i同相，电路呈电阻性。

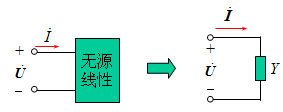
图（a）所示为一个含线性电阻、电感和电容等元件，但不含独立源的一端口N0。

当它在角频率为ω的正弦电压（或正弦电流）激励下处于稳定状态时，端口的电流(或电压)将是同频率的正弦量。

应用相量法，端口的电压相量与电流相量的比值定义为该一端口的阻抗 Z（又叫等效阻抗，输入阻抗，驱动点阻抗）。

1.Z 和总电流、总电压的关系

由复数形式的欧姆定律

可得：

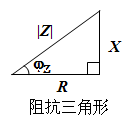
阻抗模: 　　　阻抗角:

阻抗适合于串联电路的计算,单位是欧姆。

2.单一元件的复阻抗

正弦激励下

3.Z和电路性质的关系（以RLC串联电路为例）

当信号角频率一定时，电路性质由参数决定

ω L > 1/ω C ，X>0， φZ>0，电压领先电流，电路呈感性；

ω L<1/ω C ，X<0， φZ <0，电压落后电流，电路呈容性；

ω L=1/ω C ，X=0， φZ =0，电压与电流同相，电路呈电阻性。

问题讨论：

对RLC串联电路，假设R、L、C已定，电路性质能否确定？（阻性？感性？容性？）

不能！

∵

当ω不同时，可能出现：

XL > XC ，或 XL < XC , 或 XL =XC 。

4.阻抗三角形和电压三角形的关系