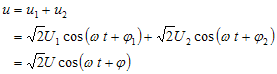西门子PLC代理商6ES7212-1BE40-0XB0

1.正弦交流电路 如果电路中激励的大小与方向均随时间按正弦规律变化,由此产生的电流、电压的大小和方向也是按正弦规律变化的,这样的电路称为正弦交流电路。 正弦交流电由交流发电机、正弦信号发生器得到。 正弦交流电的优越性: ·便于传输; ·便于运算; ·有利于电器设备的运行; · . . . . .。 2.正弦量的方向 电路中按正弦规律变化的电压或电流,统称为正弦量。 正弦交流电压、电流的实际方向是周期性变化的,在电路图上所标的方向是参考方向。
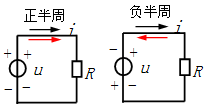
交流电路进行计算时,首先也要假设物理量的参考正方向,然后才能用数字表达式来描述。
|
1.复数的表示形式 (1)代数形式
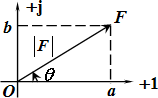
共轭复数 F*=a-jb 在数学中虚单位常用i表示,如F=a+bi,但由于在电路中已用i表示电流,故虚单位改用j表示。 实部(real part):Re[F] = a;虚部(imaginary part):Im[F] = b。 复数可用复平面上的向量表示(如图所示)。 (2)三角形式 F=|F|(cosθ+jsinθ) |F|为复数的模,θ为复数的幅角,θ=argF。则 |F|= (3)指数形式(exponential form)
(4)极坐标形式(polar form) F=|F|<θ 2.复数的基本运算 (1)加减运算 复数的加减运算采用代数形式较为简便,或在复平面中使用平行四边形法则。设F1 = a1 + jb1,F2 = a2 + jb2,有
平行四边形法则:
(2)乘除运算 复数的乘除运算使用指数形式或极坐标形式较为简便。 ①指数形式
即复数乘积的模等于各复数模的积;辐角等于各复数辐角的和。
②极坐标形式
(3)旋转因子 复数 ejθ = cosθ + jsinθ = 1∠ θ Fejθ →复数F逆时针旋转一个角度θ ,模不变
+j ,–j, -1 都可以看成旋转因子。 若一个复数乘以j,等于在复平面上把该复数逆时针旋转π/2。若一个复数除以j ,等于把该复数乘以-j ,则等于在复平面上把该复数顺时针旋转π/2。
(4)相等运算 两个复数相等必须满足: 复数的实部、虚部分别对应相等; 或者复数的模和辐角分别对应相等。 若F1 = F2,则必须有 或 |

正弦量的数学描述,可以采用正弦函数,也可采用余弦函数。
正弦量在坐标轴上可以正弦波来表示其随时间变化的图形,如上图。 三要素: Im:电流振幅 (amplitude) (*大值) ω:角频率(angular frequency) (弧度/秒) φ:初相位(initial phase angle) 正弦量一般用余弦函数来表示。 1.振幅与有效值
(1)瞬时值:正弦量在任一瞬间的值,用小写字母表示, 如i 、u。 (2)振幅:正弦量的*大值,用大写字母加下标“m”表示,如Um、Im。 (3)有效值(effective value):用大写字母表示,如U、I。 在工程应用中常用有效值U、I表示交流电压、电流的大小: ①常用交流电表指示的电压、电流读数,就是被测物理量的有效值。 ②标准电压220V,也是指正弦交流供电电压的有效值。 有效值定义:设两个相同的电阻,分别流过周期交流电流和直流电流。如果在周期信号的一个周期内,两个电阻消耗的能量相等,则该直流电流的数值为周期交流电流的有效值,表明两者在能量消耗方面具有相同的效果。 周期交流电流 i(t) 在一个周期T 时间内在电阻R上消耗的电能为:
直流电流I在一个周期T 时间内在电阻R上消耗的电能为: W2=I2RT 按照有效值的定义,若W1 = W2,则
电流的有效值是交流电流在一个周期内的均方根值。 类似地,周期电压的有效值:
正弦电流、电压的有效值 设 i(t)=Imcos(ωt+φ)
有效值的概念也适用于任何其他周期性的交流电压和电流。 问题与讨论: 若购得一台耐压为 300V 的电器,是否可用于 220V 的正弦交流线路上?
该电器*高耐压低于正弦交流电源电压的*大值,所以不能用! 2.频率与周期
(1)周期 T:变化一周所需的时间,单位:s。 (2) 频率 f:每秒变化的次数,单位:Hz。 (3)角频率ω:是正弦量的相位(ωt + φ)随时间变化的角速度(每秒变化的弧度)。即
角频率ω的单位为rad/s,与正弦量的周期T和频率f间的关系为:
小常识: (1)电网频率: 中国 50 Hz 美国 、日本 60 Hz (2)有线通讯频率:300 - 5000 Hz (3)无线通讯频率: 30 kHz - 3×104 MHz 3.初相位与相位差
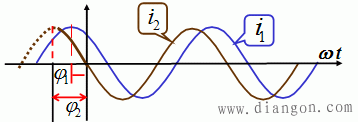
(1)相位角(或相位):(ωt + φ)。 (2)初相位: t = 0 时的相位,或称为初相角。 初相角的**值一般小于180o 即规定: |φ|≤π (180°) 说明:初相角给出了观察正弦波的起点或参考点,常用于描述多个正弦波相互间的相位关系。 (3)相位差(phase difference) : 两个同频率正弦量的相位角之差。 设: 相位差:
相位差: 同频率正弦量的相位差等于它们的初相之差,与时间无关。 电路中采用“超前”和“滞后”来说明它们相位比较的结果。 同频率正弦量的相位差可通过观察波形确定,在同一周期内两个波形的极大值(或极小值)间的角度值(≤1800),即为两者的相位差。超前者先达到极值点。 相位差与计时零点的选取、变动无关。 两种正弦信号的相位关系
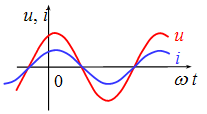
特殊相位关系: △φ= 0,称u和i同相:
△ φ=± π (±180o ) , 称u和i反相:
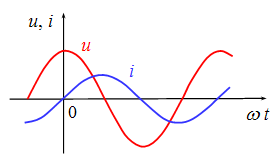
△φ=90°称u和i正交。u领先i90° 或i落后u90°
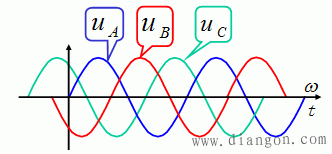
三相交流电路:三个电压初相位各差120°。
正弦量乘以常数,正弦量的微分,积分,同频率正弦量的代数和等运算,其结果仍为一个同频率的正弦量。 如: 则: 幅度、相位变化频率不变 结论: 因角频率(ω)不变,所以以下讨论同频率正弦量时,ω可不考虑,主要研究幅度与初相位的变化。 |
- 西门子中国授权代理商6ES7215-1HG40-0XB0 2023-10-26
- 西门子中国授权代理商6ES7215-1AG40-0XB0 2023-10-26
- 西门子中国授权代理商6ES7215-1BG40-0XB0 2023-10-26
- 西门子中国授权代理商6ES7214-1HG40-0XB0 2023-10-26
- 西门子中国授权代理商6ES7214-1AG40-0XB0 2023-10-26
- 西门子中国授权代理商6ES7214-1BG40-0XB0 2023-10-26
- 西门子中国授权代理商6ES7212-1HE40-0XB0 2023-10-26
- 西门子中国授权代理商6ES7212-1AE40-0XB0 2023-10-26
- 西门子中国授权代理商6ES7212-1BE40-0XB0 2023-10-26
- 西门子中国代理商6ES7215-1HG40-0XB0 2023-10-26
- 西门子中国代理商6ES7215-1AG40-0XB0 2023-10-26
- 西门子中国代理商6ES7215-1BG40-0XB0 2023-10-26
- 西门子中国代理商6ES7214-1HG40-0XB0 2023-10-26
- 西门子plc模块-驱动器代理-2023 2023-10-26
- 西门子cpu模块-驱动器代理-2023 2023-10-26
联系方式
- 地址:上海杨浦 上海市松江区广富林路4855弄88号3楼
- 邮编:200093
- 电话:15821971992
- 经理:聂聪
- 手机:15821971992
- 传真:021-33556143
- QQ:2724917714
- Email:2724917714@qq.com


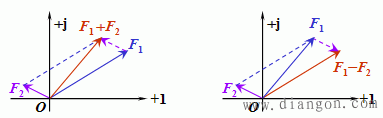
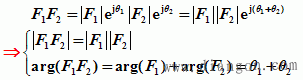
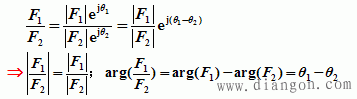
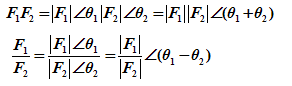
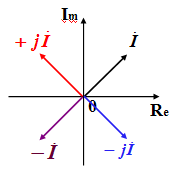
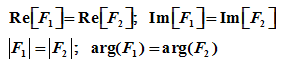


 注意:只适用正弦量。
注意:只适用正弦量。