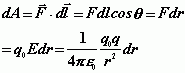6ES7313-6CG04-4AB2原理

   在静电场中取一任意闭合环路，将检验电荷从环路上任一点出发，沿移动一周又回到，电场力作功为

所以

即静电场中场强沿任意闭合环路的线积分恒等于零。这个结论叫静电场的环路定理，它说明静电场是保守力场（位场）。它是反映静电场规律的两条基本定理之一。

1、平面角    任一平面角的大小都可以用"弧度"来量度，有     当以不同的半径作圆时，角所对的弧长 与半径成正比，即2、立体角    在球面上取一面元 ，由它的边缘上各点引直线到球心，这样就构成一个锥面。这个锥面的顶角是立体的，称为立体角，用 表示。即    因为整个球面的面积是，所以它所张的立体角是球面度。当以不同的半径作同心球面时，角所对的面元与半径的平方成正比，即

1、单个点电荷的电场 
    静止的点电荷位于点，在产生的电场中，把一检验电荷从点沿任意路径移到点，当移动一位移元时，电场力所作的元功为

总功为

    可见，电场力对检验电荷所作的功与路径无关，只与起点和终点的位置有关，并与检验电荷的电量成正比。
2、任意带电体系的电场
    设有一组点电荷，在它们所激发的电场中，将检验电荷由点移动到点，在此过程中电场力所作的功为

根据场强叠加原理

其中是单独存在时所激发的场强，所以

    结论：电荷在静电场中移动时，电场力所作的功只与该电荷的起点和终点位置有关，而与路径无关。

1、均匀带电球壳的场强     设有一半径为的球壳均匀带电，其所带电量为，求球壳内外的电场强度。    解：（1）、球壳外的场强    通过点以为球心、为半径作一封闭球面为高斯面。由于对称性，该面上场强的数值都相同，方向沿半径向外。应用高斯定理，得所以   （2）、球壳内的场强    通过点以为球心、为半径作一封闭球面为高斯面。由于对称性，该面上场强的数值都相同，方向沿半径向外。应用高斯定理，得所以2、均匀带电球体的场强     设有一半径为的均匀带电球体，其所带电荷的体密度为 ，求球体内外的电场强度。    解：（1）、球体外的场强    通过点以为球心、为半径作一封闭球面为高斯面。由于对称性，该面上场强的数值都相同，方向沿半径向外。应用高斯定理，得所以   （2）、球体内的场强    通过点以为球心、为半径作一封闭球面为高斯面。由于对称性，该面上场强的数值都相同，方向沿半径向外。应用高斯定理，得所以 3、无限大均匀带电平面的场强     设有一无限大均匀带电平面，其所带电荷的面密度为 ，求带电平面的电场强度。    解：经过平面中部作一封闭圆柱面为高斯面，其轴线与平面正交，底面积为 。令为两底面上的场强，则通过的电通量为 ，由高斯定理，得所以    若有两平行无限大均匀带电平面，其所带电荷的面密度为。可以证明，在两平行板中间，电场强度为    在两平行板外侧，电场强度为4、无限长均匀带电直导线的场强    设有一无限长均匀带电直导线，其所带电荷的线密度为，求带电导线周围的电场强度。    解：过直导线作一高为、截面半径为r 的封闭圆柱面为高斯面。根据电场轴的对称性，通过圆柱侧面的电通量为，通过圆柱底面的电通量为0。由高斯定理，得所以