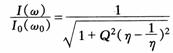6ES7313-6CG04-4AB1





题目:有两个电阻并联,R1=2Ω,R2=18Ω,电源电压为126V。求总电阻R和总电流I以及两支路电流I1和I2,如图所示; 解题:由公式: (2×18)÷(2+18)=36÷20=1.8Ω(并联电路总电阻),总电流等于电压被总电阻除(欧姆定律),即: I=U/R=126÷1.8=70A 流过R1的电流I1=U/R1=126÷2=63A,流过R2的电流I2=U/R2=126÷18=7A。 |
并联从字面上理解便是并在一起的连接,有两个以上的电阻,他们的一端接在一起,另一端也连接在一起,两个节点是以外加的电压,形成一个又分支的电路,这就叫做并联电路。如上图中的两个灯泡便是并联关系,当然了控制灯泡的两个开关相互之间也是并联。 并联电阻及电流和电压的大小
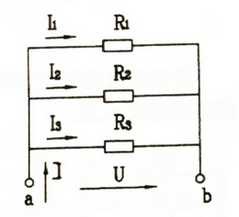
并联电路电压:由于各个支路一段连接在一起,另一端也连接在一起,承受同一电源的电压,所以各支路的电压是相同的。 并联电路电流:由于各个支路电压相等,根据欧姆定律便可知电阻小的支路电流大;电阻大的支路电流小。即并联各支路的电流与对应的电阻成反比分配; 因为:I1=U/R1;I2=U/R2;I3=U/R3 并联电路电功率:由于各个并联支路电压相同,各支路电流又与电阻成反比分配,所以各个支路电功率与电阻也成反比例分配; P1:P2:P3=U/R1:U/R2:U/R3=1/R1:1/R2:1/R3 并联电路总电流:根据基尔霍夫电流定律知,并联电路总电流等于各支路电流之和: I=I1+I2+I3 并联电路电阻:并联电路总电阻的倒数等于各支路电阻倒数之和,证明如下: 因为:I=I1+I2+I3 所以: 在实际电路中,常遇到两个电阻并联的电路,这时总电阻可以用下式计算:
当R1≥R2时;两个组织相差很悬殊的电阻并联后,其等值电阻更接近与小电阻值。当R1=R2时,R=R1÷2,如果有n个阻值相同的电阻并联,其等值电阻值为:R=R1÷n。这说明并联电阻数越多,等值电阻越小。 若总电流为已知,则分电流可由下式计算:
|
1、谐振 正弦稳态电路中,电流与电压一般相位不同,若电压超前电流 处在谐振状态的电路称为谐振电路 2、RLC串联谐振电路 输入阻抗 谐振条件
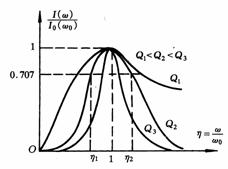
谐振角频率 串联谐振电路的电路参量 串联谐振电路的谐振特点: 1)电压与电流同相位, 2)当输入电压 3)电感电压 RLC并联电路与RLC串联电路是对偶电路,利用对偶关系,可以很方便得到RLC谐振并联谐振电路的特点。 3、并联谐振 如图1所示并联谐振电路,输入导纳 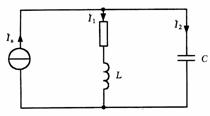 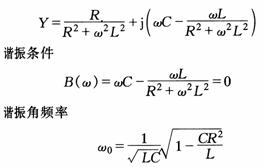 4、串、并联谐振电路的频率特性
为了通用性和分析比较不同的电路频率特性问题的方便,一般采用归一化处理,得到归一化幅频特性等。如RLC串联电路中电流
由此可见,谐振电路的通频带与Q值成反比。 |
联系方式
- 地址:上海杨浦 上海市松江区广富林路4855弄88号3楼
- 邮编:200093
- 电话:15821971992
- 经理:聂聪
- 手机:15821971992
- 传真:021-33556143
- QQ:2724917714
- Email:2724917714@qq.com

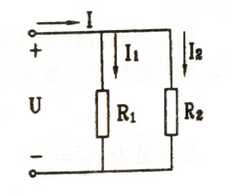
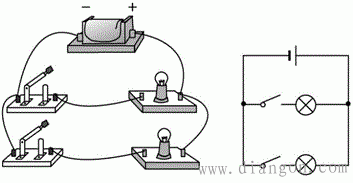
 这里用右图来说明并联电路的特点。
这里用右图来说明并联电路的特点。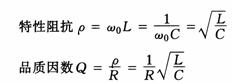
 正弦电流电路中电流、电压、阻抗、导纳等物理量随频率变化的特性称为频率特性。这些量的模和辐角与频率的关系又分别称为幅频特性和相频特性。
正弦电流电路中电流、电压、阻抗、导纳等物理量随频率变化的特性称为频率特性。这些量的模和辐角与频率的关系又分别称为幅频特性和相频特性。