西门子模块一级代理|授权代理商-大量现货






1.测量不确定度 测量不确定度表示测量结果(测量值)不能肯定的程度,是可定量地用于表达被测参量测量结果分散程度的参数。这个参数可以用标准偏差表示,也可以用标准偏差的倍数或置信区间的半宽度表示。 2.标准不确定度 用被测参量测量结果概率分布的标准偏差表示的不确定度就称为标准不确定度,用符号u表示。 测量结果通常由多个测量数据子样组成,对表示各个测量数据子样不确定度的标准偏差,称为标准不确定度分量,用ui表示。标准不确定度有A类和B类两类评定方法。 A类标准不确定度是指用统计方法得到的不确定度,用符号uA表示。 B类标准不确定度是指用非统计方法得到的不确定度,即用根据资料或假定的概率分布估计的标准偏差表示的不确定度,称为B类标准不确定度,用符号uB表示。A类标准不确定度和8类标准不确定度仅评定方法不同。 3.合成标准不确定度 由各不确定度分量合成的标准不确定度,称为合成标准不确定度。当间接测量时,即测量结果是由若干其他量求得的情况下,测量结果的标准不确定度等于各其他量的方差和协方差相应和的正平方根,用符号uC表示。合成标准不确定度仍然是标准(偏)差,表示测量结果的分散性。这种合成方法,通常被称为“不确定度传播律”(过去有的地方也称其为“误差传播定律”,其实所传播的并不是误差,而是不确定度。现在均改称为“不确定度传播定律”)。 4.扩展不确定度 扩展不确定度是由合成标准不确定度的倍数表示的测量不确定度。它用覆盖因子k乘以合成标准不确定度得到以一个区间的半宽度来表示的测量不确定度。覆盖因子k是为获得扩展不确定度,而与合成标准不确定度相乘的数字因子,它的取值决定了扩展不确定度的置信水平。通常k取2~3之间的某个值,类似于前面误差理论中的置信因子。扩展不确定度是测量结果附近的一个置信区间,被测量的值以较高的概率落在该区间内,用符号U表示。通常测量结果的不确定度都用扩展不确定度U表示。 当说明具有置信概率为P的扩展不确定度时,可以用Up表示,此时覆盖因子也相应地以kP表示。例如,U0.99表示测量结果落在以U为半宽度区间的概率为0.99。 U和uC作单独定量表示时,数值前可不加正负号。注意测量不确定度也可以用相对形式表示。 |

当在测量数据中发现某个数据可能是异常数据时,一般不要不加分析就轻易将该数据直接从测量记录中删除,**能分析出该数据出现的主客观原因。判断粗大误差可从定性分析和定量判断两方面来考虑。 定性分析就是对测量环境、测量条件、测量设备、测量步骤进行分析,看是否有某种外部条件或测量设备本身存在突变而瞬时破坏;测量操作是否有差错或等精度测量过程中是否存在其他可能引发粗大误差的因素;也可由同一操作者或另换有经验操作者再次重复进行前面的(等精度)测量,然后再将两组测量数据进行分析比较,或再与由不同测量仪器在同等条件下获得的结果进行对比,以分析该异常数据出现是否“异常”,进而判定该数据是否为粗大误差。这种判断属于定性判断,无严格的规则,应细致和谨慎地实施。 定量判断,就是以统计学原理和误差理论等相关专业知识为依据,对测量数据中的异常值的“异常程度”进行定量计算,以确定该异常值是否为应剔除的坏值。这里所谓的定量计算是相对上面的定性分析而言,它是建立在等精度测量符合一定的分布规律和置信概率基础上的,因此并不是**的。 下面介绍两种工程上常用的粗大误差判断准则。 1.拉伊达准则 拉伊达准则是依据对于服从正态分布的等精度测量,其某次测量误差|Xi-X0|大于3σ的可能性仅为0.27%。因此,把测量误差大于标准误差σ(或其估计值
式中,Xk为被疑为坏值的异常测量值; 当某个可疑数据Xk的 拉伊达准则是以测量误差符合正态分布为依据的,值得注意的是一般实际工程等精度测量次数大都较少,测量误差分布往往和标准正态分布相差较大;因此,在实际工程应用中当等精度测量次数较少(例如n≤20)时,仍然采用基于正态分布的拉伊达准则,其可靠性将变差,且容易造成3 2.格拉布斯(Grubbs)准则 格拉布斯准则是以小样本测量数据,以t分布(详见概率论或误差理论有关书籍)为基础用数理统计方法推导得出的。理论上比较严谨,具有明确的概率意义,通常被认为实际工程应用中判断粗大误差比较好的准则。 格拉布斯准则是指小样本测量数据中某一测量值满足表达式
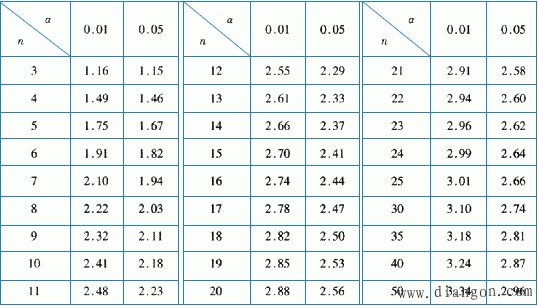
式中,Xk为被疑为坏值的异常测量值; 当某个可疑数据Xk的 格拉布斯准则的鉴别值KG(n,α)是和测量次数n、危险概率α相关的数值,可通过查相应的数表获得。表1是工程常用α=0.05和α=*在不同测量次数n时,对应的格拉布斯准则鉴别值KG(n,α)表。 当α=0.05或*时,按测量数据个数n查表1得到格氏准则作为粗大误差的判别的鉴别值KG(n,α)的置信概率P分别为0.95和0.99。即按(2)式得出的测量值大于按表1-1查得的鉴别值KG(n,α)的可能性仅分别为0.5%和1%,这说明该数据是正常数据的概率已很小,可以认定该测量值为含有粗大误差的坏值并予以剔除。 表1 KG (n,α)数值表
应注意的是,若按式(1-22)和表1-1查出多个可疑测量数据时,不能将它们都作为坏值一并剔除,每次只能舍弃误差*大的那个可疑测量数据,如误差超过鉴别值KG(n,α)*大的两个可疑测量数据数值相等,也只能先剔除一个,然后按剔除后的测量数据序列重新计算 格拉布斯准则是建立在统计理论基础上,对n<30的小样本测量较为科学、合理的判断粗大误差的方法。因此,目前国内外普遍推荐使用此法处理小样本测量数据中的粗大误差。 如果发现在某个测量数据序列中,先后查出的坏值比例太大,则说明这批测量数据极不正常,应查找和消除故障后重新进行测量和处理。 |
联系方式
- 地址:上海杨浦 上海市松江区广富林路4855弄88号3楼
- 邮编:200093
- 电话:15821971992
- 经理:聂聪
- 手机:15821971992
- 传真:021-33556143
- QQ:2724917714
- Email:2724917714@qq.com