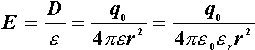将一电池与电容器相连，电池给电容器充电。在某一瞬间，电容器带电量、极板间电位差为时，将电量由电容器的负极移到正极时，电源克服电场力作功为这也是移动电荷时外力所作的功。

    而，在电量由的整个充电过程中，外力所作的总功为

    这功应转变为电容器所储存的能量，用表示。利用电容的定义，我们可以把上面的结果改写为

所以，电容也是反映电容器储存能量本领大小的物理量。

而

两式整理后，得

如果定义一点的电位移矢量为

则有

上式称为有介质存在时的高斯定理。因为是电位移矢量的通量，所以它可以表述为：通过任一闭合曲面的电位移通量，等于包围在该闭合面内自由电荷的代数和。

     2、关于定理的几点说明
　　（1）有介质存在时的高斯定理是更普遍的规律，它概括了真空中的高斯定理。
　　（2）在的高斯定理中，和不直接出现，在电荷和介质分布具有一定对称性的情况下，可以由自由电荷的分布，求出的分布。
　　（3）高斯面上任一点的是由空间总的自由电荷的分布决定，不能认为只与面内自由电荷有关。 

一、极化的微观机制
1、无极分子的位移极化 
    在外电场作用下，无极分子正负电荷“中心”发生相对位移而出现极化电荷的现象，称为位移极化。
2、有极分子的取向极化 
    在外电场作用下，有极分子的电偶极矩受到电场的力矩而转向外电场，在垂直于外电场方向的两端面上也出现极化电荷的现象，称为取向极化。
二、极化强度矢量
1、定义
　　在介质中取一无限小体积元，设 内分子电偶极矩的矢量和为，则定义极化强度矢量为

    也就是说，极化强度矢量等于单位体积内所有分子电偶极矩的矢量和。它是描述介质内部极化程度的物理量。单位：库/米2 ( C/m 2 )。
    若介质内部各点的大小、方向均相同，则称为均匀极化。在真空和处于静电平衡状态的导体中，没有极化电荷，所以。

2、与极化电荷的关系　

    在介质中取一个长为 底面积为 的圆柱截面。    由于圆柱体体积很小，其内 可看作常数。整个圆柱体内电偶极矩的总和为所以，圆柱体表面极化电荷面密度为

写成矢量形式，得

为介质表面法线的单位矢量。

    若与之间夹角 ，则 

    若与之间夹角 ，则

    若与之间夹角 ，则