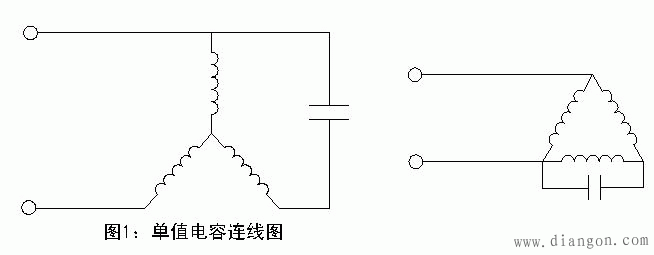
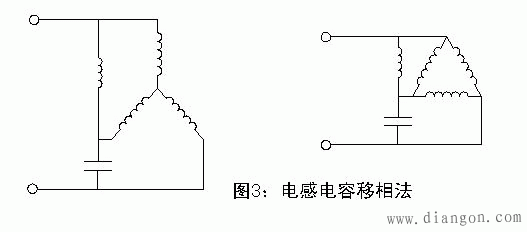
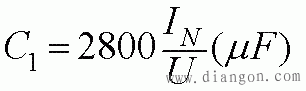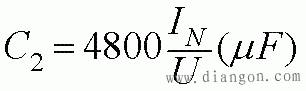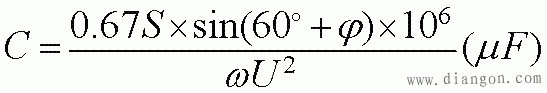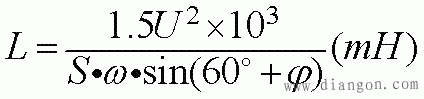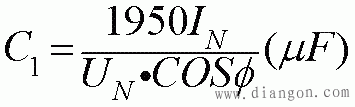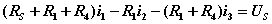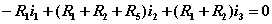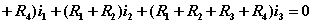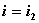如电网容量允许，几千瓦的三相电机可改为单相运行，但电机的功率将有所下降，三相电流不平衡性加剧，易引起电机过热。
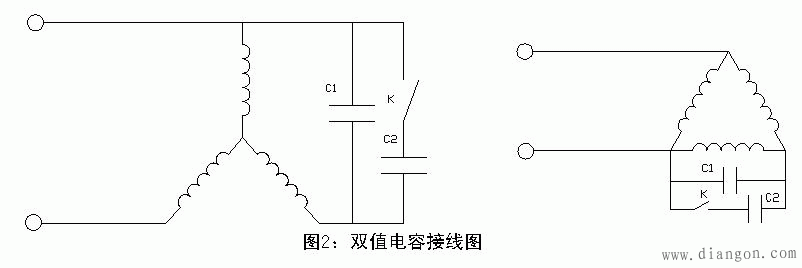
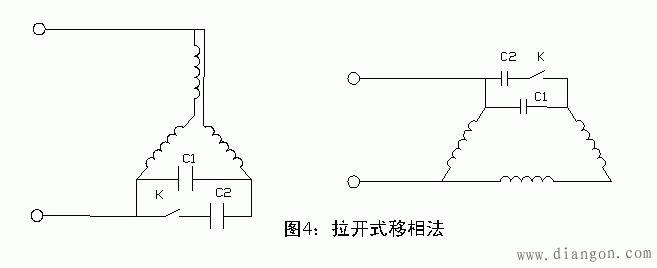
2、双值电容
C2＝（2～3）C1（μF），Uc＝1.15U（V）
C2＝（2～3）C1（μF），Uc＝1.15U（V）
C：运行电容（μF），U：单相电源电压（V），ψ＝arccosφ，cosφ是电动机功率因数，S：三相视在功率（VA），ω＝2πf。
C1：运行电容，C2：起动电容
IN、UN：电动机额定电流，额定电压； |
为减少未知量 ( 方程 ) 的个数，假想每个基本回路中有一个回路电流沿着构成该回路的各支路流动。各支路电流用回路电流的线性组合表示。来求得电路的解。
1. 回路电流法
以基本回路中的回路电流为未知量列写电路方程分析电路的方法。当取网孔电流为未知量时，称网孔法。
|
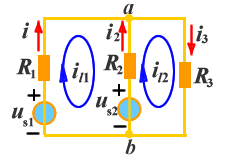
1）支路电流与回路电流的关系
上图所示电路有两个独立回路，选两个网孔为独立回路，设网孔电流沿顺时针方向流动，如图所示。可以清楚的看出，当某支路只属于某一回路（或网孔），那么该支路电流就等于该回路（网孔）电流，如果某支路属于两个回路（或网孔）所共有，则该支路电流就等于流经该支路两回路（网孔）电流的代数和。如上图电路中：
 |
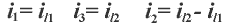2）回路电流法列写的方程
回路电流在独立回路中是闭合的，对每个相关节点回路电流流进一次，必流出一次，所以回路电流自动满足KCL。因此回路电流法是对基本回路列写KVL方程，方程数为：b-(n-1)
与支路电流法相比，方程数减少n-1个。
2.方程的列写
应用回路法分析电路的关键是如何简便、正确地列写出以回路电流为变量的回路电压方程。以上图电路为例列写网孔的KVL方程，并从中归纳总结出简便列写回路KV方程的方法。
按网孔列写 KVL 方程如下：
| 网孔1： |  |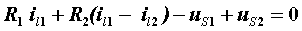
| 网孔2： |  |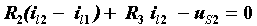
将以上方程按未知量顺序排列整理得：
 |
 |
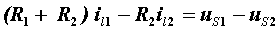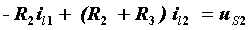观察方程可以看出如下规律：
第一个等式中，il1前的系数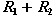 
是网孔1中所有电阻之和，称它为网孔1的自电阻，用R11表示；il2前的系数
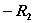是网孔1和网孔2公共支路上的电阻，称它为两个网孔的互电阻，用R12表示，由于流过R2的两个网孔电流方向相反，故R2前为负号；等式右端
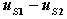表示网孔1中电压源的代数和，用uS11表示，uS11中各电压源的取号法则是，电压源的电压降落分向与回路电流方向一致的取负号，反之取正号。用同样的方法可以得出等式2中的自电阻、互电阻和等效电压源分别为：
| 自电阻 | 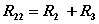 | 互电阻 | 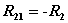 | 等效电压源 |  |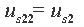
由此得回路（网孔）电流方程的标准形式：
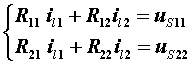
结论：对于具有l=b-(n -1) 个基本回路的电路，回路（网孔）电流方程的标准形式:
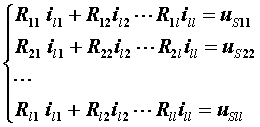
其中: 自电阻Rkk为正；
互电阻 Rjk＝Rkj可正可负，当流过互电阻的两个回路电流方向相同是为正，反之为负；
等效电压源uSkk中的电压源电压方向与该回路电流方向一致时，取负号；反之取正号。
注：当电路不含受控源时，回路电流方程的系数矩阵为对称阵。
回路法的一般步骤：
(1) 选定l=b-(n -1)个基本回路，并确定其绕行方向；
(2) 对l个基本回路，以回路电流为未知量，列写 KVL 方程；
(3) 求解上述方程，得到l个回路电流；
(4) 求各支路电流(用回路电流表示 ) ；
(5) 其它分析。
注：电路中含有理想电流源和受控源时，回路方程的列写参见例题。
例题 列写如下电路的回路电流方程，说明如何求解电流 i.
 |
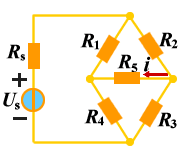解1：
独立回路有三个。选网孔为独立回路如图所示，回路方程为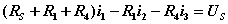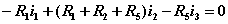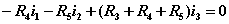：   从以上方程中解出网孔电流1和网孔电流2，则电流  |  |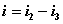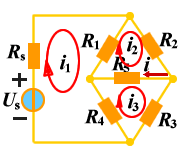
选网孔为独立回路 |
注：本题结果说明：
(1)不含受控源的线性网络，回路方程的系数矩阵为对称阵，满足 Rjk = Rkj。
(2)当网孔电流均取顺时针或逆时针方向时，Rjk均为负。
解2：
为了减少计算量，可以只让一个回路电流经过R5支路如图所示。此时回路方程为： |  |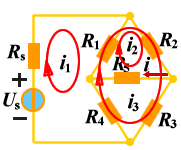
一个回路电流经过R5支路 |
注：解法2的特点是计算量减少了，但互有电阻的识别难度加大，易遗漏互有电阻。本题也说明独立回路的选取有多种方式，如何选取要根据所求解的问题具体分析。
1. 网络图论 图1 a 哥尼斯堡七桥b 对应的图 19～20世纪，图论主要研究一些游戏问题和古老的难题，如哈密顿图及四色问题。1847年，基尔霍夫首先用图论来分析电网络，如今在电工领域，图论被用于网络分析和综合、通讯网络与开关网络的设计、集成电路布局及故障诊断、计算机结构设计及编译技术等等。 2. 电路的图 a 电路图b 电路的图(一个元件作为一条支路)c 电路的图(采用复合支路) 图2电路和电路的图 有向图――标定了支路方向（电流的方向）的图为有向图。 图3 有向图图4 非连通图图5 连通图 子图――若图G1中所有支路和结点都是图G中的支路和结点，则称G1是图G的子图。 a 电路的图（G）b G图的子图c G图的子图 图6 树（T）——树（T）是连通图G的一个子图，且满足下列条件： 图7 电路的图与树的定义 需要指出的是： 图8电路的图与回路定义 基本回路(单连支回路)――基本回路具有独占的一条连枝色，即基本回路具有别的回路所没有的一条支路。 图9 电路的图及其基本回路 结论：电路中结点、支路和基本回路关系为：支路数＝树枝数＋连支数＝结点数－1＋基本回路数 b=n+l-1 |
- 西门子一级|驱动器总代商|2023 2023-10-26
- 西门子plc模块|驱动器总代理|2023 2023-10-26
- 西门子plc模块-驱动器代理 2023-10-26
- 西门子cpu模块-驱动器代理 2023-10-26
- 西门子一级-驱动器代理 2023-10-26
- 西门子cpu模块-驱动器代理商 2023-10-26
- 西门子一级-驱动器代理商 2023-10-26
- 西门子plc模块|驱动器总代理商 2023-10-26
- 西门子cpu模块|驱动器总代理商 2023-10-26
- 西门子一级|驱动器总代理商 2023-10-26