正弦交流电的这些表示方法能表现出正弦交流电的瞬时值随时间变化的规律。

解析法是用数学公式表述正弦交流电与实践变化关系的方法。公式如下：

e=Emsin（ωt+Φe）

u=Umsin（ωt+Φu）

i=Imsin（ωt+Φi）

它可以表达正弦量的*大值、初相角和周期。由上述公式可知，只要知道一个正弦量的*大值，初相角和频率，一个正弦量即完整的被确定，因此：

通常把：*大值、初相角、角频率叫做正弦交流电的三要素。

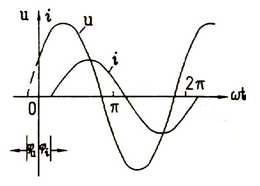
正弦曲线图示法即利用平面直角坐标系中的横坐标表示时间t，纵坐标表示正弦量的瞬时值，并根据解析式的计算，用绘制出的正弦曲线图来表达正弦量的方法，如右图所示。

正弦交流电还可以用旋转矢量法表示。什么是旋转矢量呢？

如右图所示，从原点出发作一有向线段，令它的长度等于正弦量的*大值Im，与水平轴的夹角等于正弦量的初相位Φ，并以等于正弦量角频率的角速度ω逆时针旋转，则在任一瞬间，该有向线段在纵轴上的投影就等于该正弦量的瞬时值Imsin（ωt+Φ）。这样的有向线段就叫做旋转矢量。

正弦交流电的电压、电流和电动势都可以用旋转矢量表示，要进行同频率正弦量的加减运算时，可以先做出各个正弦量对于的旋转矢量，然后按照平行四边形法则求出合成旋转矢量，这合成旋转矢量的长度就是总的正弦量的*大值，合成旋转矢量与轴OX（横轴）的夹角就是总正弦量的初相位。

从上右图中可以看到，用旋转矢量来表示正弦量通常是很繁琐的，一般情况下：

我们只用有向线段的初始位置（t=0的位置）来表示正弦量，即吧有向线段的长度表示为正弦量的大小，把有向线段与横轴正向的夹角表示正弦量的初相位，这种表示正弦量的方法叫做相量法。

如果使有向线段的长度等于正弦量的*大值，这种相量称为正弦量的*大值相量，以符号Em、Um、Im表示。在实际问题中，我们遇到的往往是正弦量的有效值，如果使用有向线段的长度等于正弦量的有效值，这种相量叫做有效值相量，用符号U、E、I表示。几个同频率的相量画在同一个相量图中，可以按矢量合成的方法对相量进行加减运算。