假定对某个被测参量进行等精度(测量误差影响程度相同)重复测量n次,其测量示值分别为X1、X2、…,Xi、…,Xn、则各次测量的测量误差,即随机误差(假定已消除系统误差)分别为
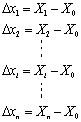 (1)
(1)
式中,X0为真值。
如果以偏差幅值(有正负)为横坐标,以偏差出现的次数为纵坐标作图。可以看出,随机误差整体上均具有下列统计特性:
(1)有界性 即各个随机误差的**值(幅度)均不超过一定的界限;
(2)单峰性 即**值(幅度)小的随机误差总要比**值(幅度)大的随机误差出现的概率大;
(3)对称性 (幅度)等值而符号相反的随机误差出现的概率接近相等;
(4)抵偿性 当等精度重复测量次数n→∞时,所有测量值的随机误差的代数和为零,即
![]()
所以,在等精度重复测量次数足够大时,其算术平均值![]() 就是其真值X0较理想的替代值。
就是其真值X0较理想的替代值。
大量的试验结果还表明:测量值的偏差——当没有起决定性影响的误差源(项)存在时,随机误差的分布规律多数都服从正态分布;当有起决定性影响的误差源存在,还会出现诸如均匀分布、三角分布、梯形分布、t分布等。下面对正态分布、均匀分布作简要介绍。
1.正态分布
高斯于1795年提出的连续型正态分布随机变量并的概率密度函数表达式为:
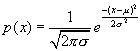 (2)
(2)
式中,μ为随机变量的数学期望值;e为自然对数的底;σ为随机变量x的均方根差或称标准偏差(简称标准差);
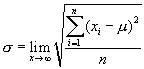 (3)
(3)
σ2为随机变量的方差,数学上通常用D表示;n为随机变量的个数。
其中,μ和σ是决定正态分布曲线的两个特征参数。其中μ影响随机变量分布的集中位置,或称其正态分布的位置特征参数;σ表征随机变量的分散程度,故称为正态分布的离散特征参数。μ值改变,σ值保持不变,正态分布曲线的形状保持不变而位置根据μ值改变而沿横坐标移动,如图2所示。当μ值不变,σ值改变,则正态分布曲线的位置不变,但形状改变,如图2所示。σ值变小,则正态分布曲线变得尖锐,表示随机变量的离散性变小;σ值变大,则正态分布曲线变平缓,表示随机变量的离散性变大。
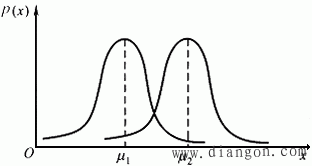
图1 μ对正态分布的影响示意图
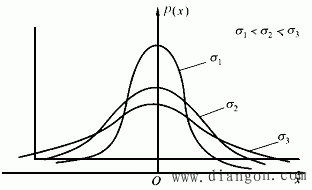
图2 σ对正态分布的影响示意图
在已经消除系统误差条件下的等精度重复测量中,当测量数据足够多时,测量的随机误差大都呈正态分布,因而完全可以参照式(1)的高斯方程对测量随机误差进行比较分析。
分析测量随机误差时,标准差d表征测量数据离散程度。σ值愈小,则测量数据愈集中,概率密度曲线愈陡峭,测量数据的精密度越高;反之,σ值愈大,测量数据愈分散,概率密度曲线愈平坦,测量数据的精密度越低。
2.均匀分布
在测试和计量中,随机误差有时还会服从非正态的均匀分布等。从误差分布图上看,均匀分布的特点是:在某一区域内,随机误差出现的概率处处相等,而在该区域外随机误差出现的概率为零。均匀分布的概率密度函数φ(x)为
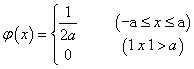 (3)
(3)
式中a为随机误差x的极限值。
均匀分布的随机误差概率密度函数的图形呈直线,如图3所示。
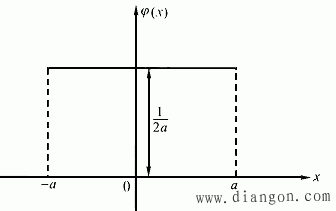
图3 均匀分布曲线
较常见的均匀分布随机误差通常是因指示式仪器度盘、标尺刻度误差造成的误差,检测仪器*小分辨力限制引起的误差,数字仪表或屏幕显示测量系统产生的量化(±1)误差,智能化检测仪器在数字信号处理中存在的舍人误差等。此外,对于一些只知道误差出现的大致范围,而难以确切知道其分布规律的误差,在处理时亦经常按均匀分布误差对待。
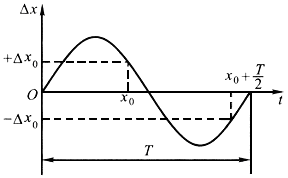
在测量过程中,若发现测量数据中存在系统误差,则需要作进一步地分析比较,找出产生该系统误差的主要原因以及相应减小系统误差的方法。由于产生系统误差的因素众多,且经常是若干因素共同作用,因而显得更加复杂,难以找到一种普遍有效的方法来减小和消除系统误差。下面几种是*常用的减小系统误差方法。 1.针对产生系统误差的主要原因采取相应措施 对测量过程中可能产生的系统误差的环节作仔细分析,找出产生系统误差的主要原因,并采取相应措施是减小和消除系统误差*基本和*常用的方法。例如,如果发现测量数据中存在的系统误差的原因主要是传感器转换过程中存在零位误差或传感器输出信号与被测参量间存在非线性误差,则可采取相应措施调整传感器零位,仔细测量出传感器非线性误差,并据此调整线性化电路或用软件补偿的方法校正和消除此非线性误差。如果发现测量数据中存在的系统误差主要是因为信号处理时采用近似经验公式(如略去高次项等),则可考虑用改进算法、多保留高次项的措施来减小和消除系统误差。 2.采用修正方法减小恒差系统误差 利用修正值来减小和消除系统误差是常用和非常有效的方法之一,在高精度测量、计量与标定时被广泛采用。 通常的做法是在测量前预先通过标准器件法或标准仪器法比对(计算),得到该检测仪器系统误差的修正值,制成系统误差修正表;然后用该检测仪器进行具体测量时可人工或由仪器自动地将测量值与修正值相加,从而大大减小或基本消除该检测仪器原先存在的系统误差。 除通过标准器件法或标准仪器法获取该检测仪器系统误差的修正值外,还可对各种影响因素,如温度、湿度、电源电压等变化引起的系统误差,通过反复实验绘制出相应的修正曲线或制成相应表格,供测量时使用。对随时间或温度不断变化的系统误差,如仪器的零位误差、增益误差等可采取定期测量和修正的方法解决。智能化检测仪器通常可对仪器的零位误差、增益误差间隔一定时间自动进行采样并自动实时修正处理,这也是智能化仪器能获得较高测量精度的主要原因。 3.采用交叉读数法减小线性系统误差 交叉读数法也称对称测量法,是减小线性系统误差的有效方法。如果检测仪器在测量过程中存在线性系统误差,那么在被测参量保持不变的情况下其重复测量值也会随时间的变化而线性增加或减小。若选定整个测量时间范围内的某时刻为中点,则对称于此点的各对测量值的和都相同。根据这一特点,可在时间上将测量顺序等间隔对称安排,取各对称点两次交叉读入测量值,然后取其算术平均值作为测量值,即可有效地减小测量的线性系统误差。 4.采用半周期法减小周期性系统误差 对周期性系统误差,可以相隔半个周期进行一次测量,如图1所示。取两次读数的算术平均值,即可有效地减小周期性系统误差。因为相差半周期的两次测量,其误差在理论上具有大小相等、符号相反的特征,所以这种方法在理论上能很好地减小和消除周期性系统误差。
图1 半周期法读数示意图 以上几种方法在具体实施时,由于种种原因都难以完全消除所有的系统误差,而只能将系统误差减小到对测量结果影响*小以至可以忽略不计的程度。 如果测量系统误差或残余系统误差代数和的**值不超过测量结果扩展不确定度(有关内容详见本章第五节)的*后一位有效数字的一半,通常就认为测量系统误差已经很小,可忽略不计了。 |